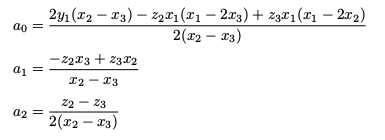Linear Function
Consider a function of the form y = a1x + a0 where a1 ≠ 0.
Two Points
If two distinct points (x1,y1) and (x2,y2) are known and x1 ≠ x2, then the coefficients are given by
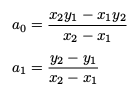
One Point and a Slope (Gradient)
If one point (x1,y1) is known, along with the slope (gradient) m, then the coefficients are given by
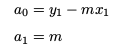
Quadratic Function
Consider a function of the form y = a2x2 + a1x + a0 where a2 ≠ 0.
Three Points
If three distinct points (x1,y1), (x2,y2) and (x3,y3) are known and x1 ≠ x2 ≠ x3 ≠ x1, then the coefficients are given by
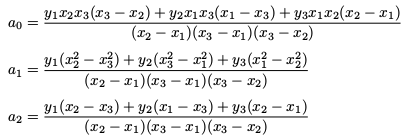
Two Points and a Slope (Gradient)
If two distinct points (x1,y1) and (x2,y2) are known with x1 ≠ x2, along with the slope z3 at x = x3 with x3 ≠ (x1 + x2)/2, then the coefficients are given by
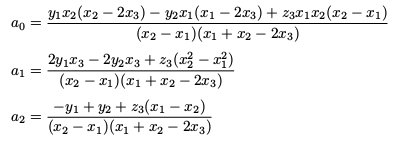
One Point and Two Slopes (Gradients)
If one point (x1,y1) is known, along with the slopes z2 at x = x2 and z3 at x = x3 (x2 ≠ x3), then the coefficients are given by